Mixture of expert explanation

What's new behind Mixture of expert (MoE) mechanism? [Part 1]

TLDR; In middle of the trend of scaling language model, Mixture of Expert (MoE) is a potential candidate to replace current scaling method and achieve comparable score to close-source LLMs like GPT-3.5, GPT-4, Claude, etc. Mixtral 8x7B is the latest open-source model from Mistral and took the spotlight on several open LLM benchmarks until this day (03/2024). In this blog, I will dig into the technique behind the success of MoE and try my best to give you all you need to know about MoE.

What is Mixtral 8x7B

In the LLMs marathon, Mixtral 8x7B leads the open-source benchmark in various chatbot categories. It boasts triple the votes of the 2nd open-source LLM and trails behind GPT-4, OpenAI’s strongest LLM (by ~ 45 points)https://openlm.ai/chatbot-arena/. Mixtral 8x7B is the next version of Mixtral 7B, developed by the Mistral AIhttps://mistral.ai/ team. The difference between the Mixtral 8x7B and other transformer models is the high-quality of the sparse mixture of expert layers (MoE) attachment.

The table below presents the strength of Mixtral 8x7B when compared with LLaMA 2 (the latest open-source LLM from Meta) and GPT-3.5 (the most common LLM from OpenAI).

Mixture of Experts report (source: mixtral-of-expertshttps://mistral.ai/news/mixtral-of-experts/)

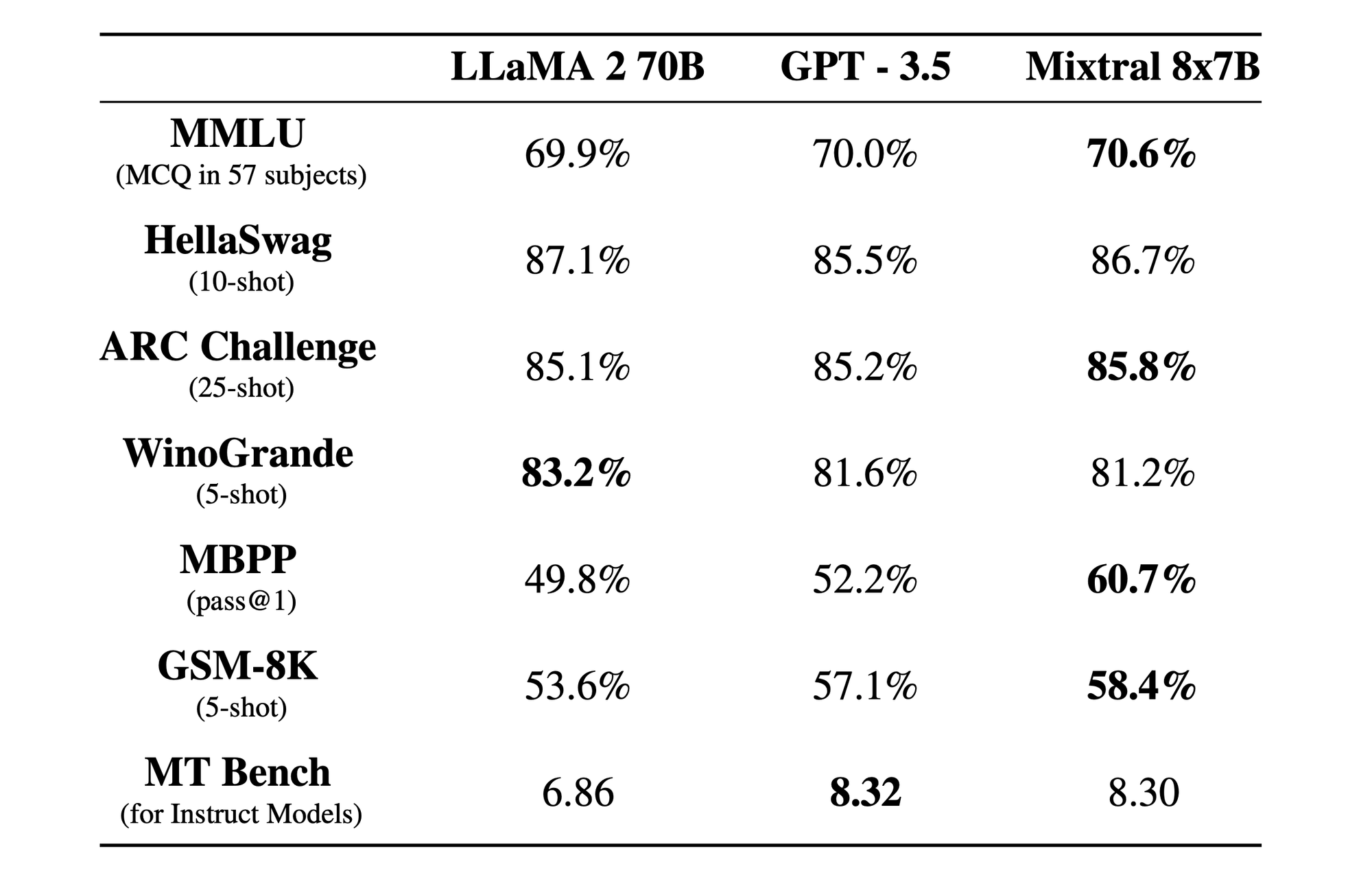
Mixtral 8x7B supports upto 32k tokens in term of context length, pre-train natively with 5 natural languages (i.e English, French, Italian, German and Spanish), releases under Apache 2.0 and allows people to commercialize it.

Mixtral also proved to be good at coding, which achieved 40.2% on HumanEval. The development team also released an Instruct version of Mixtral, which has been optimized through fine-tuning and DPO to follow instructions given by the user.

Mixture of Expert

Behind the success of mixtral 8x7B is mixture of expert (MoE) architecture. MoE bring to current transformers model the ability to speed up twice inferencing and pre-training time due to the token path in expert layer require only certain node to work at a time. The current work also found out MoE with instruction tuning is promising.

Definition of Sparse model

The sparse model is a combination of 2 parts: (1) a gate network (router) and (2) expert layers.

• Sparse of MoE layer: Instead of using a normal feed-forward neural layer (FFN) inside transformer encoder or decoder, they replace it by a Sparse of MoE layer which contain a define number of experts, which in practice is actually FFN, but they can be also replace with any complex layer.

Illustration of an MoE layer. For each input x, the router will only select one expert to perform computations. The choice is based on the output of the gating network (dotted line). The expert layer returns the output of the selected expert (gray box) multiplied by the route gate value (softmax of the gating function output). (Source: )

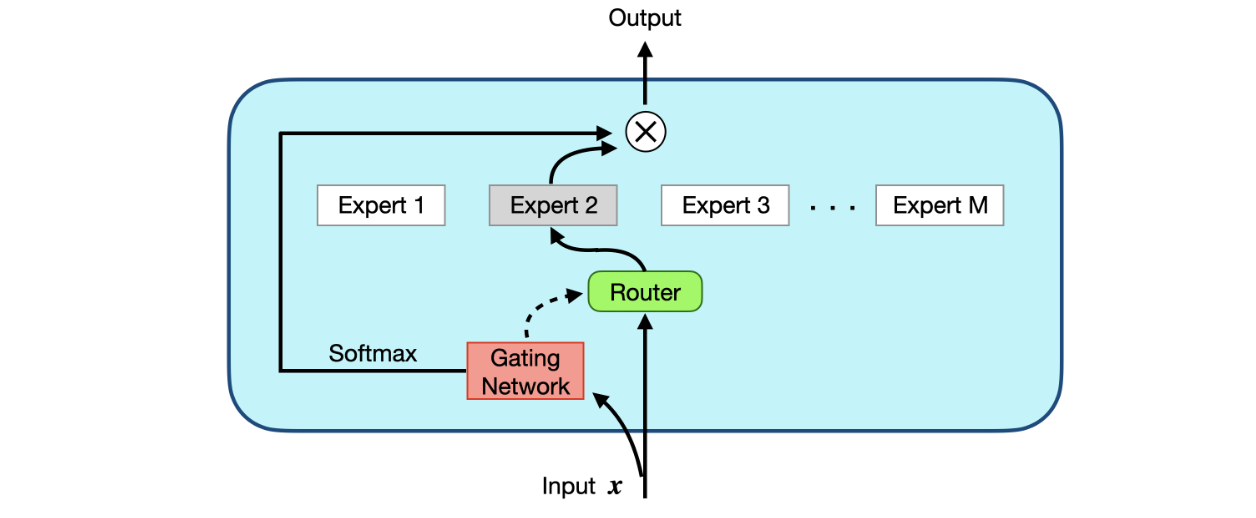
• Gate network or Router: A router will be used to determine which token will be sent to which expert. We can also send tokens to more than 1 expert. By the route system of gate neural, after training, each expert can specialize in a specific portion of the data.

We can denote the MoE layer as follow:

\[y = \sum^{n}_{i=1}G(x_i)E_i\]

where \(G\) present Gate neural network and \(E_i\) indicate expert \(i^{th}\). With \(M\) is total number of expert layers, if \(n\) is equal to whole expert set (\(n=M\)), this is called soft routing (\(T_i=[N]\), at the moment \(i\), tokens is sent to \(N\) expert). But soft routing is not efficiency compare with dense model, therefor “switch routing” are replaced to save computation time and make the gating network sparse.

Inside MoE layer contain \(M\) expert, switch routing model will pick 1 expert from \(M\) at each time \(T_i=[1]=argmax_m({h_m(x; \Theta)})\).

In practice, if \(G\) is 0, the correspond expert operation is saving from computing. In a traditional setup, a softmax function can be added as a gating function (Wg is a trainable weight matrix multiplied by the input x):

\[G_{\sigma}(x)=Softmax(x.W_g)\]

The Gate network is so good so far, however, you might encouter with the question “what if the number of training token is spent to each expert not equal?”. Yes, it does. To purchase load-balancing for all experts, in Shazzer’s work , they added an additional trainable noise, i.e., Gaussian noice \(H(x)\). And a “keep” function to store only the top k values and set the rest to \(-\infty\) cause the gate values to equal 0, denoted as \(KeepTopK()\).

\[H(x)_i=(x.W_g)_i+StandardNormal().Softplus((x.W_{noise})_i)\] \[KeepTopK(v,k)_i = \begin{cases}v1 &\text{if } v_i \text{ is in the top } k \text{ elements of } v \\-\infty & \text{other}\end{cases}\]

Therefore: $G(x) = Softmax(KeepTopK(H(x), k))$

Since we introduced discontinuities in the output of the Gating function, however, this is fine. Don’t take my words, Shazzer said, “they observed this to be no problem in practice at all, and they trained the gating network by simple back-propagation, along with the rest of the model.”

Addressing Challenges of MoE

Discontinuities in Routing

While sparse routing model saves computation and greatly reduces the inference times, it also causes discontinuities in routing. From the beginning, they added independently Gaussian noise \(H(x)_i = (x.W_g)_i + StandardNormal()\), but in practice, they showed that even a small perturbation of the gating network outputs may change the router behavior drastically.

From there, we can think of a additional loss function to allow the expert to receive roughly equal numbers of training example. However, when the training example come with a discrete quantity, it can not be used in back propagation. The problem can be solved by adding a smooth transition (smooth estimator \(Load(X)\)) between different routing behaviors (to make the router more stable).

Balancing Expert Utilization

From the beginning, all experts initialize the same weights and training algorithm is the same. It is hard for new gating network learn right feature since every router is zero. Therefore, a mistake in training at the beginning may cause the expert to amplify that mistake.

In Zixiang’s work , they investigate the effectiveness of the initialization into expert divergence, they analyze the MoE layer between a stage called exploration stage where start at \(t=0\) and ends at \(T_1 = [\eta^-1\sigma_0^0.5]\), at each time one expert from \(M\) experts is picked and with the gating network remains nearly unchanged. Even under the same treatment condition in each expert node, result shows after the exploration stage the experts become specialized to some specific task only based on the initialization.